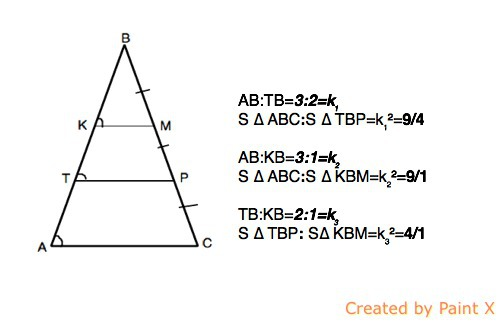
Пусть исходный треугольник будет АВС, а пересекают его прямые КМ и ТР, параллельные АС.
КМ ║ТР║ АС⇒ соответственные углы, образованные при их пересечении секущей АВ, равны, а угол В для всех трех треугольников общий.
∆ АВС ~ ∆ТВР~∆ КВМ по двум углам, прилежащим к одной стороне.
АВ=3 части, ТВ=2 части. КР=1 часть.
Отношение площадей подобных фигур равно квадрату коэффициента их подобия.
АВ:ТВ=3:2=k₁
S ∆ ABC:S ∆ TBP=k₁²=9/4
AB:KB=3:1=k₂
S ∆ ABC:S ∆ KBM=k₂²=9/1
TB:KB=2:1=k₃
S ∆ ТВР: S∆ КВМ=k₃²=4/1