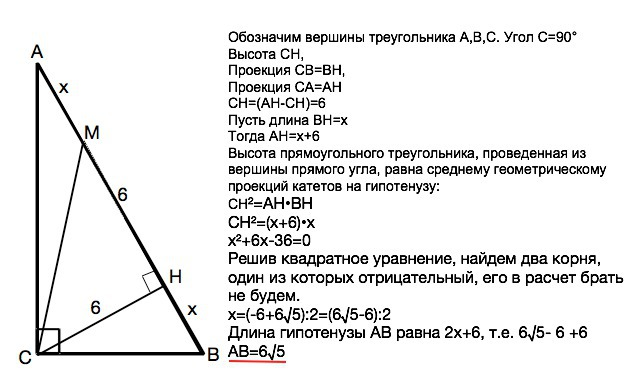
Обозначим вершины треугольника А,В,С. Угол С=90°
Высота СН,
ВН - проекция катета СВ
АН - проекция катета СА
СН=(АН-СН)=6
Пусть длина ВН=х
Тогда АН=х+6
Высота прямоугольного треугольника, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу:
СН²=(х+6)•х ⇒
х²+6х-36=0
Решив квадратное уравнение, найдем два корня, один из которых отрицательный, его в расчет брать не будем.
х=(-6+6√5):2=(6√5-6):2
Длина гипотенузы АВ равна 2х+6, т.е. 6√5- 6 +6
АВ=6√5