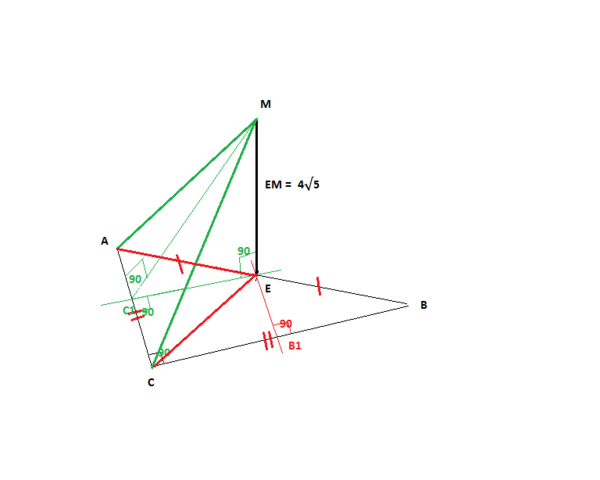
сделаем построение по условию
гипотенуза АВ
угол
ЕМ = 4√5
АС=ВС=16см <----катеты равны </span>
треугольник равнобедренный , значит
ПРОВЕДЕМ из точки Е перпендикуляр ЕB1 до прямой BС
ЕB1 || AC и т. Е - середина АВ -значит ЕB1 -средняя линия
EB1 = 1/2*AC =1/2*16 = 8 см <---<span>в)Расстояние между прямыми ЕМ и ВС
ПРОВЕДЕМ из точки Е перпендикуляр ЕС1 до прямой АС
ЕС1 || BC и т. Е - середина АВ -значит ЕС1 -средняя линия
EC1 = 1/2*CB =1/2*16 = 8 см
проведем наклонную МС1 - по теореме о тех перпендикулярах МС1 тоже перпендикулярна к АС - значит это и есть расстояние от точки М до прямой АС
тогда треугольник МЕС1 - прямоугольный
по теореме Пифагора
MC1^2 = ЕM^2 +EC1^2 = (4√5)^2 + 8^2 = 144
MC1 =12 см <-------a)</strong>
в треугольнике АСМ
МС1 - высота
точка С1 - середина АС - значит равнобедренный AM = MC
площадь треугольника АСМ S(ACM) =1/2*AC*MC1 =1/2*16*12=96 см2
его проекции на плоскость - это треугольник АЕС с высотой ЕС1 и основанием АС
площадь проекции Sпр = 1/2*EC1*AC =1/2*8*16 = 64 см2