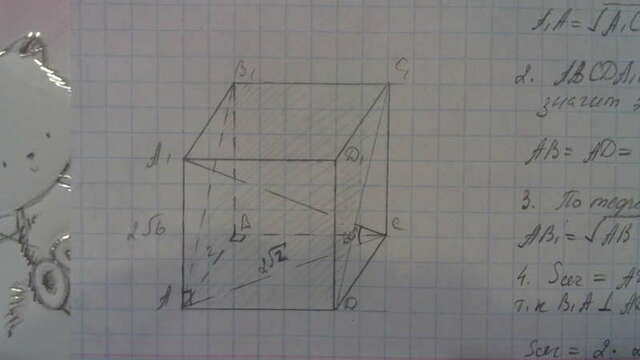
Дано: ABCDA1B1C1D1 - правильная чет. призма; угол А1СА = 60 градусов; АС = 2 корня из 2 - диагональ основания, AB1C1D - сечение призмы.
Найти: Sсеч.
Решение:
1. Рассмотрим треугольник АА1С:
треуг. АА1С - прямоуг.
а) cos60 = AC/A1C ( АС - катет, А1С - гипотенуза)
А1С = АС/cos60 = (2koren iz 2) / (1/2) = 4 kornya iz 2
б) по теореме Пифагора найдем АА1:
АА1^2 = A1C^2 - AC^2 = 32-8 = 24 => AA1 = 2корня из 6
2. ABCDA1B1C1D1 - правильная чет. призма => ABCDA1B1C1D1 - куб. => AB=AD=2 (ABCD - КВАДРАТ)
3. По теореме Пифагора найдем АВ1:
АВ1^2 = AB^2+BB1^2 = 4+24 = 28 => AB1 = 2корня из 7
4. Sсеч. = AD*AB1 [т.к. AB1C1D - прямоугольник: т.к. В1А перпендикулярен AD(по теореме о 3х перпендикулярах) и AD//B1C1]
Sсеч. = 2*2корня из 7 = 4корня из 7 см^2
Ответ: 4 корня из 7
...если ошиблась где-то, прошу прощенья...