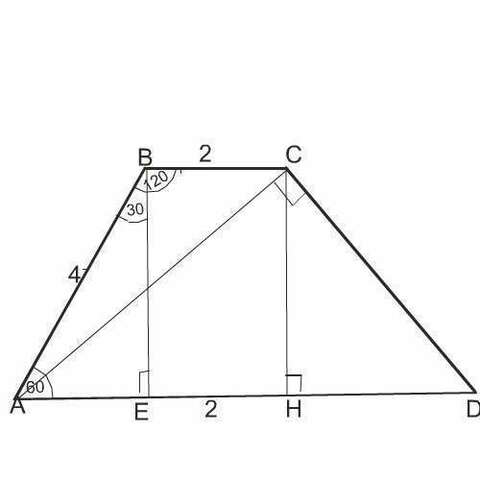
В трапеции АВСD угол АВС равен 120°
Так как сумма углов трапеции, прилежащих к одной боковой стороне, равна 180°,
угол ВАС=60°.
Опустив из вершины В высоту ВЕ к АD, получим прямоугольный треугольник с углом
∠ АВЕ=30°.
Отрезок АЕ большего основания равен половине стороны АВ и равен 2.
Высота трапеции ВЕ равна АВ*sin( 60°) =4√3):2=2√3
Опустим из С высоту СН к АD.
Отрезок ЕНравен основанию ВС трапеции и равен 2, а
АН =2+2=4
По условию задачи ∠ АСD - прямой ( обозначено на вложенном рисунке)
Высота прямоугольного треугольника, проведенная из вершины прямого угла,
есть среднее пропорциональное между отрезками, на которые делится
гипотенуза этой высотой.
СН, как высота трапеции, равна ВЕ и равна 2√3
СН²=АН*НD
12=4*D
НD=3
АD=АН+НD=7
Ответ:АD=7