Для решения подобных задач есть, если можно так сказать, классический способ.
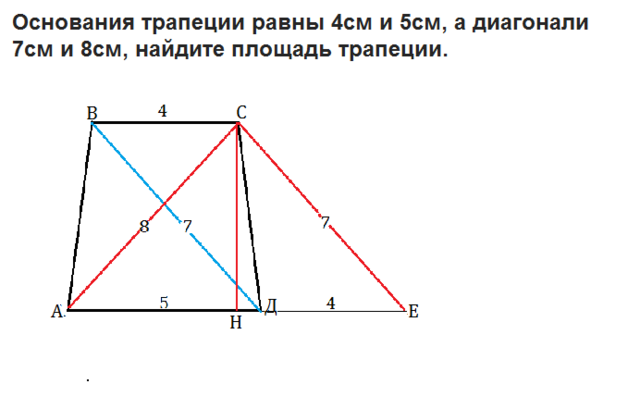
Обозначим вершины трапеции АВСД.
Из вершины С параллельно диагонали ВД проводится прямая до пересечения с продолжением АД в точке Е.
ВС|| АЕ по условию, ВД||СЕ по построению. ⇒
ВСЕД - параллелограмм, ⇒
ДЕ=ВС=4 см.
Тогда АД=5+4=9 см
В треугольнике АСЕ известны три стороны.
Площадь этого трегугольника равна площади данной трапеции. Действительно,
Ѕ (АВСД)=Н*(ВС+АД):2
Ѕ (АСЕ)=Н*(ВС+АД):2
Вычислив по
формуле Герона площадь треугольника АСЕ, тем самым найдем площадь трапеции АВСД.
Ѕ=√(р*(р-а)*р-b)*(p-c)) где a,b,c - стороны треугольника, р - полупериметр.
р=Р:2=(8+7+9):2
=12 см
Ѕ АВСД=√(12*4*5*3)=√(36*4*5)=
12√5 см² или ≈26,8328 см²
---------Вариант решения. Можно опустить высоту СН, выразить ее квадрат по т. Пифагора из прямоугольных треугольников АСН и ЕСН и приравнять это значение, приняв АН=х, НЕ=9-хЗатем по т. Пифагора из любого из треугольников найти высоту и затем площадь трапеции. Этот способ более длинный и вычислений больше, но именно так, когда это необходимо, можно найти высоту.