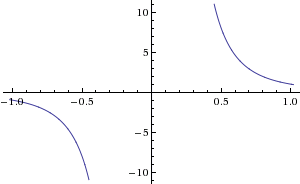найти плошадь фигуры, ограниченной линиями: 1) y=³√x, x= -8, x= -1, y=0 2) y=1/x^3, x=...

1)строим график(во вложениях)

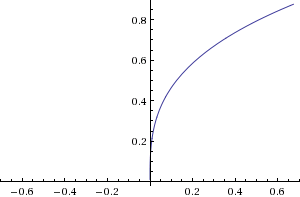
график y=³√x выше графика y=0

площадь находится как интегралл от разностей от графиков: из графика, который выше, вычетаем график, который ниже. пределы интегрирования x=-8, x=-1

$S=\int\limits^{-1}_{-8}{(\sqrt[3]{x}-0)}=(\frac{3x^\frac{4}{3}}{4})\limits^{-1}_{-8}=\frac{3}{4}-\frac{3*16}{4}=\frac{3(1-16)}{4}=-11,25\\$

2)строим график.(во вложениях) нам нужен промежуток от -3 до -1. значит график y=0 будет выше.

находим интеграл от разностей графиков с пределами -3 и -1

$S=\int\limits^{-1}_{-3}{(0-\frac{1}{x^3})}dx=-\frac{x^{-2}}{-2}=(\frac{1}{x^2})|\limits^{-1}_{-3}=\frac{1}{1}-\frac{1}{3}=\frac{2}{3}$