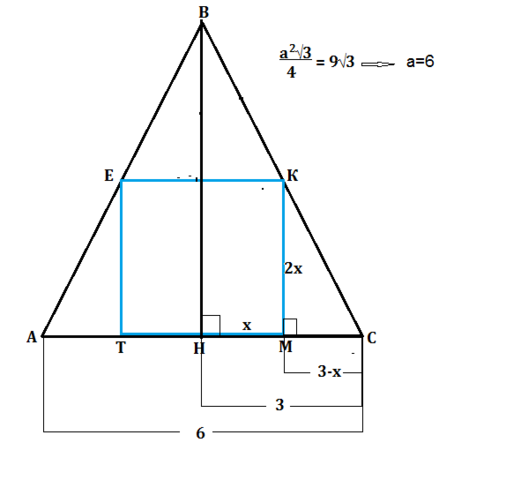
Квадрат, вырезаемый из пластины, имеющей форму правильного треугольника, должен быть вписанным в нее, чтобы иметь наибольшую площадь. Любой другой будет иметь меньшую длину стороны.
Найдем сторону правильного треугольника, выразив ее из формулы площади правильного треугольника.
9√3=(a² √3):4
36√3=a²√3
a=√36=6
АС=6, НС=3
Пусть треугольник будет АВС, его высота -ВH, вписанный в него квадрат - ЕКМТ.
Примем половину стороны квадрата равной
х, тогда КМ=2х,
Треугольники ВНС и КМС подобны - оба прямоугольные и имеют общий угол С.
ВН=ВС*sin 60º=
3√3
МС=НС-НМ=
3-х
Из подобия треугольников следует
ВН
:КМ=НС
:МС
(3√3):2х=3:(3-х)
6х=9√3-х*3√3
Сократим на 3 обе части уравнения
2х=3√3-х√3
2х+х√3==3√3
х(2+√3)=3√3
х=3√3 :(2+√3)
Домножим числитель и знаменатель правой части уравнения на (2-√3)
х=3√3 *(2-√3):(2+√3)*(2-√3)
х=3√3 *(2-√3):(4-3)
2х=6√3 *(2-√3)=12√3-18
Р=4*(12√3-18)=
48√3-72