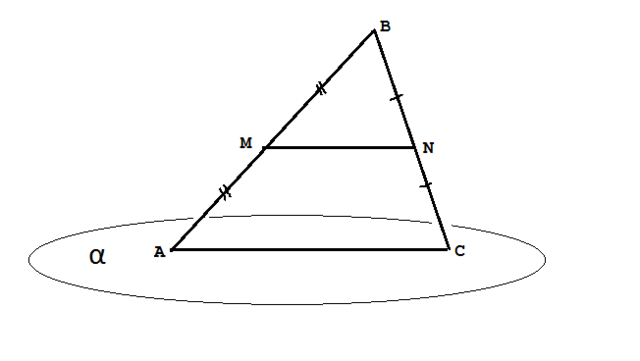
Через три точки, не лежащие на одной прямой, можно провести плосксть, притом только одну. Отсюда следует, что, так как вершина В треугольника не лежит в плоскости α, то плоскость треугольника не лежит в плоскости α, и его средняяо линия не лежит в той плоскости.
Пусть М делит пополам сторону АВ, а N- делит пополам сторону ВС
Отрезок MN-, соединяющий середины сторон треугольника, является его средней линией.
Средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей стороне и равна ее половине. (свойство средней линии)
По теореме о параллельности прямой и плоскости:
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
MN не лежит в плоскости α и параллельна АС, лежащей в плоскости α. Значит, MN || α, что и требовалось доказать.