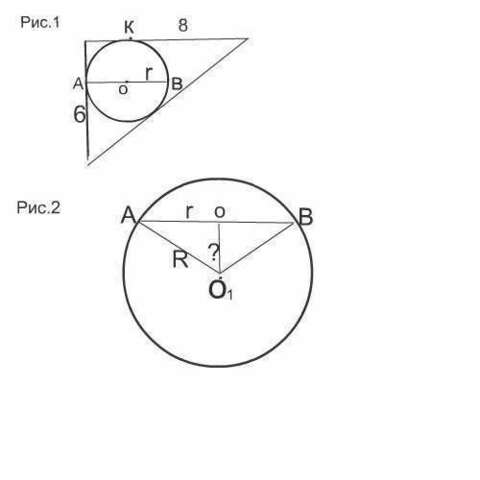
Рисунок делала до получения результата решения, поэтому он не совсем соразмерный ответу, но это ни на что не влияет.
Данный в задаче прямоугольный треугольник проводит в сфере сечение, которое принадлежит плоскости треугольника.
Расстояние от центра сферы до плоскости треугольника=расстояние от центра сферы до плоскости получившегося сечения.
Это сечение - круг, вписанный в данный треугольник.= (см.Рис.1)
Радиус r сечения найдем по формуле
r=(а+b-с):2, где а и b катеты, с - гипотенуза.
Гипотенузу найдем по теореме Пифагора:
с²=6²+8²
с=√100=10 см
r=(8+6-10):2=2 см
Сделаем рисунок сечения сферы.
В нем АВ -диаметр сечения.
Соединив центр сферы с концами диаметра, получим равнобедренный треугольник АО1В
(см. рис. 2)
О1о в нем - высота, равная расстоянию от центра сферы до плоскости сечения.
Из прямоугольного треугольника АоО1 найдем расстояние О1о.
О1о =√(R²-r²)= √(200 - 4)=14 cм