Задание 4
a₁=-9,6
a₂=-8,3
d=a₂-a₁=-8,3-(-9,6)=9,6-8,3=1,3

Найдем при каких n члены прогрессии меньше 0

a₁+1,3·(n-1)<0<br>-9,6+1,3·(n-1)<0<br>n<8,03...<br>Всего 8 слагаемых отрицательны, начиная с 9-го положительны
 Задание5
Задание5
Раскрываем знак модуля по определению
Если
х-х²≥0, то | x-x²|=x-x²
если
х-х²<0, то |x-x²|=-x+x²<br> - + -
------------(0)---------(1)---------------
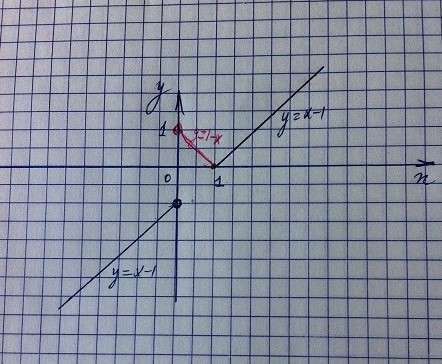
На (0;1] строим график функции

На (-∞;0)U(1;+∞) строим график функции

x≠0
поэтому при х=0 и слева и справа от 0 точки графика изображается пустыми кружками
см. рисунок в приложении
Задание 6.
Пусть первый рабочий выполняет всю работу за х часов, второй - за у часов.
Примем всю работу за 1.
Тогда

часть выполняет первый за час,

часть выполняет второй за час

Умножим второе уравнение на 6

и вычтем из второго уравнения первое

у=30
х=20
Ответ. Первый рабочий выполняет всю работу за 20часов, второй - за 30 часов.