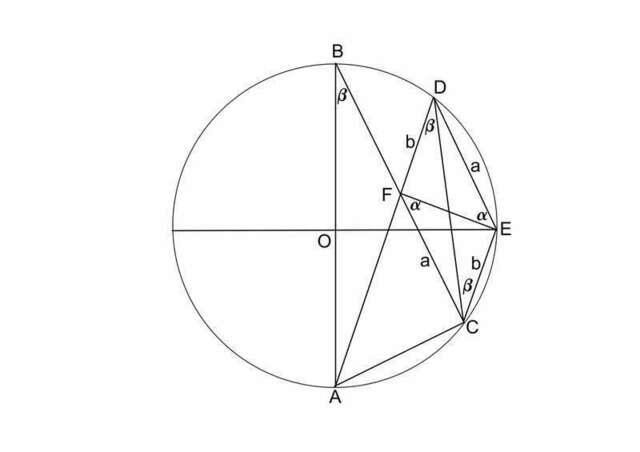
Треугольник ACF - прямоугольный и равнобедренный. Поэтому углы при его основании 45°. ∠BCE тоже равен 45°, поскольку это вписанный угол, опирающийся на четверть окружности. То есть ∠BCE = ∠AFC, и следовательно, AD II CE;
Кроме того, дуга CD также составляет 90°, и равна дуге BE; следовательно, равны дуги CE и BD, заключенные между хордами BC и DE; то есть эти хорды также параллельны.
Таким образом, фигура FCED - параллелограмм.
Более того, углы этого параллелограмма ∠FDE = ∠FCE = 45°; ∠CFD = ∠CED = 135°;
Кроме того, ∠ADC = ∠ABC; Этих условий достаточно, чтобы выразить ∠CFE через ∠ABC. Ничего больше в этой задаче сделать не получится - этот угол зависит от положения точки C на окружности.
Пусть стороны параллелограмма FC = ED = a; EC = FD = b;
Углы ∠CEF = α; ∠FDC = ∠ABC = β; тогда
a/sin(β) = b/sin(45° - β);
a/sin(135° - α) = b/sin(α);
sin(β)/sin(45° - β) = sin(45° + α)/sin(α); дальше - только важное
2 = (1 + ctg(α))*(1 - ctg(β));
ctg(α) = (1 + ctg(β))/(1 - ctg(β));
как-то так. Я мог где-то ошибиться, на ходу делал, так что тщательно проверьте всё :).
Можно это привести к тангенсам.