Решается методом интервалов.
Для того, чтобы дробь из трех членов была меньше или равна нулю, надо чтобы нечетное число членов было меньше нуля. При этом члены в числители могут быть равны нулю. А вот выражение в знаменателе не может быть равно нулю, иначе дробь превращается в бесконечность.
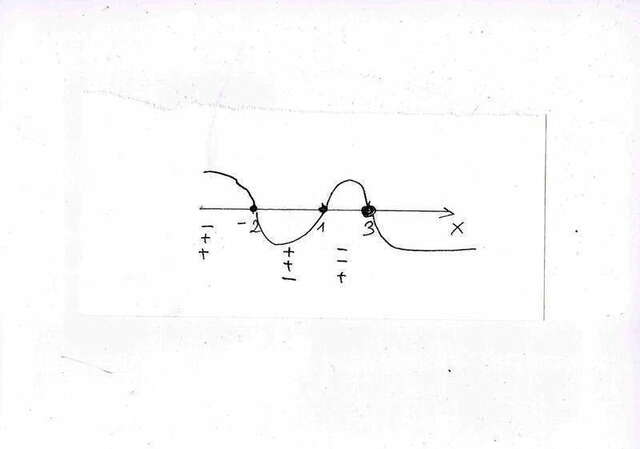
У нас есть три знакопеременных точки: x=1, x=-2 и x=3
Делаем рисунок.
Мы подставили в выражение значения из каждого интервала и получили, что искомому неравенству удовлетворяют интервалы от -2 до 1 и от 3 (выколотая точка) до +∞.
Ответ: x∈[-2;1]∨(3;+∞)