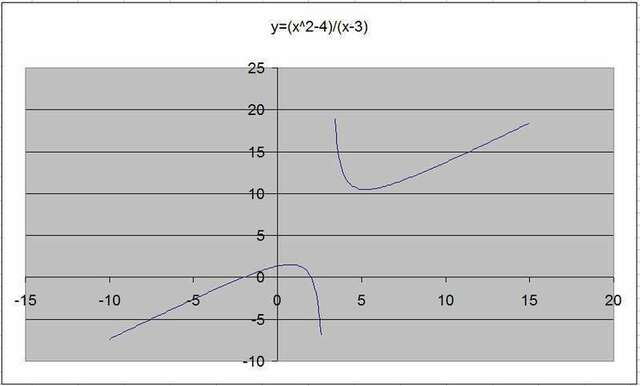
У(x)=(х^2-4)/(x-3)
1)ОДЗ x-3 не равно 0 -> x є (-беск ; 3) U (3;+беск)
2)график имеет вертикальную асимптоту х=3
3)нули функции у(x)=(х^2-4)/(x-3)=(х-2)*(х+2)/(x-3)=0 при х=-2 и при х = 2
4)асимптота вида у = ах+в
у(x)=(х^2-4)/(x-3) = у=(х^2-3х+3х-12+12-4)/(x-3) = х + 3+ 8/(х-3)
a = lim y(x)/x = lim( (х + 3+ 8/(х-3)) : x ) = 1
b = lim (y(x) - a*x) = lim (х + 3+ 8/(х-3) - 1*x) = lim ( 3+ 8/(х-3)) = 3
наклонная асимптота вида у = ах+в
у=х+3
5)экстремумы
у(x)= х + 3+ 8/(х-3)
у`(x)= 1 - 8/(х-3)^2
у`(x)=0 при х=3 + (+/-) корень(8)
x1 =3 - корень(8)
x2 =3 + корень(8)
у``(x)= 16/(х-3)^3
у``(x1)= 16/(х1-3)^3=-16/(8)^(3/2) < 0 -> x1 - точка локального максимума
у``(x2)= 16/(х2-3)^3=16/(8)^(3/2) > 0 -> x2 - точка локального максимума
6)перегибы
уравнение у``(x)= 16/(х-3)^3=0 - не имеет решений -> график перегибов не имеет
7)четность
у(-х)=((-х)^2-4)/((-x)-3) = -(х^2-4)/(x+3)
у(-х) - не равно у(х)
у(-х) - не равно -у(х)
функция у(х) не является ни четной ни нечетной
8) не периодичная так как имеется ограниченное и ненулевое число экстремумов