Сначала рассмотрим вариант равнобедренной трапеции с боковыми сторонами 6 и 6, и основаниями 10 и 4.
Отсюда средняя линия равна:

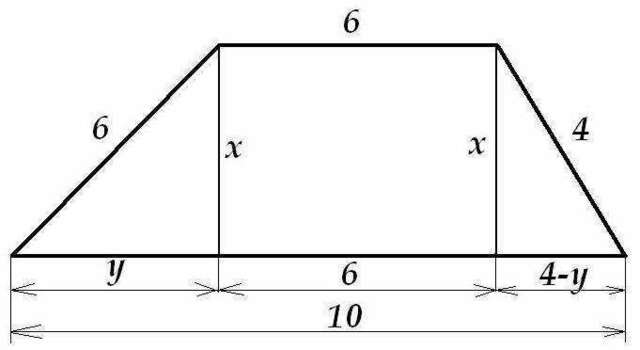
Теперь рассмотрим вариант существования трапеции с основаниями 10 и 6, и боковыми сторонами 4 и 6, и выявим её внешний вид:
Расписывать долго не буду, смотрим рисунок:
Пусть на рисунке трапеция с основаниями 10 и 6, и боковыми сторонами 4 и 6. Все обозначения на рисунке, поехали:

Выразим из обоих уравнений  и приравняем полученные выражения между собой:
и приравняем полученные выражения между собой:


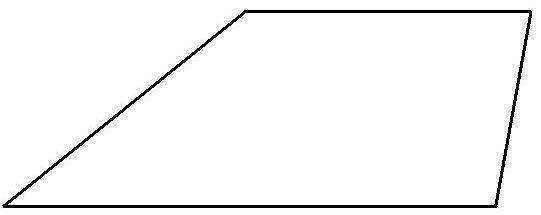
 - один из катетов меньшего треугольника, значит трапециия с параллельными сторонами 10 и 6, и двумя другими 6 и 4 будет иметь примерно такой вид, как на втором рисунке, что называется тупоугольной трапецией.
- один из катетов меньшего треугольника, значит трапециия с параллельными сторонами 10 и 6, и двумя другими 6 и 4 будет иметь примерно такой вид, как на втором рисунке, что называется тупоугольной трапецией.
Средняя линия такой трапеции равна: