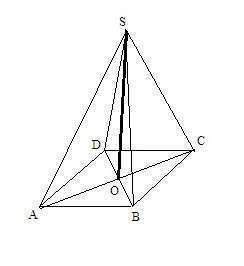
Нам дана 4-угольная пирамида, у которой все ребра равны.
Значит, в основании у нее лежит квадрат. Пусть сторона квадрата равна а.
Радиус круга, в который вписан квадрат, равен R = a/√2 = a√2/2
Боковые ребра пирамиды тоже равны а. Найдем ее высоту.
Отрезок ОА от центра основания до угла равен радиусу, R = a/√2.
OAS - это прямоугольный треугольник, AS = a; OA = a/√2.
OS = H = √(AS^2 - OA^2) = √(a^2 - a^2/2) = √(a^2/2) = a/√2 = R
Высота пирамиды равна радиусу описанной окружности ее основания.
Это и означает, что этот радиус и есть радиус шара.
То есть центр основания совпадает с центром шара.