Сделать чертёж и вычислить площадь фигуры ограниченной линии y=6x-x 2-5, Ox

$y=6x-x^2-5\\ y=-x^2+6x-5$

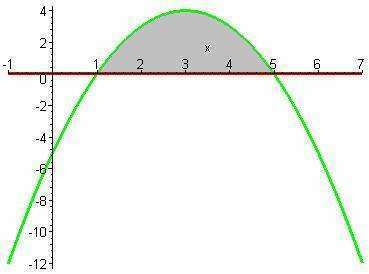
График - парабола, ветви её направлены вниз (коэффициент при икс квадрат отрицательный).

Координаты вершины параболы:

$x_0=-\frac{b}{2a}=\frac62=3,\\ y_0=-\frac{D}{4a}=-\frac{b^2-4ac}{4a}=-\frac{36-4\cdot1\cdot5}{4(-1)}=\frac{16}4=4$

То есть, вершина параболы находится в точке (3;4).

Найдём точки пересечения параболы с осями координат:

$c\;OY,\;x=0\\ y=-0+0-5=-5\\ c\;OX,\;y=0\\ -x^2+6x-5=0\\ D=16=4^2\\ x_1=1,\;x_2=5$

Сделаем чертёж (см.рис. - искомая фигура обозначена серым цветом). Парабола находится выше оси OX, поэтому площадь фигуры будем искать по формуле

$\int\limits_b^a(-x^2+6x-5-0)dx$

Точки пересечения с осью ОХ - это пределы интегрирования. a=1, b=5

$\int\limits_1^5(-x^2+6x-5)dx=-\frac13x^3+3x^2-5x|\limits_1^5=\\ =-\frac13\cdot125+3\cdot25-5\cdot5+\frac13-3+5=-\frac{125}3+\frac13+52=\\ =-41\frac13+52=8\frac23$