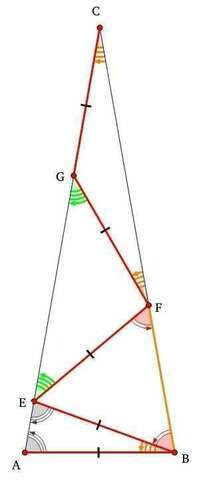
Очевидно, что, если AB = BE = EF = FG = GC, то треугольники AEB, EFB, EGF и GCF будут равнобедренными, ∠ACB будет равен ∠GCF и ∠GFC и, по подобию треугольников, равен ∠ABE, а треугольник ВEF — равносторонний, т.е. все углы его по 60º. Зная, что сумма углов треугольника подчиняется равенству ∠ACB + ∠CBA + ∠BAC = 180º, а для равностороннего треугольника ABC, у которого ∠CBA = ∠BAC = ∠FBE + ∠EBA, справедливо ∠AСB + 2∠ВAС = ∠AСB + 2(∠FBE + ∠EBA) = ∠AСB + 2(60º + ∠AСB) = 180º. Проверяя предложенные варианты решения задачи, получаем:
а) при ∠AСB=15º -> 15º + 2(60º + 15º) = 165º — не соблюдается сумма углов треугольника 180º — вариант не верен;
б) при ∠AСB=36º -> 36º + 2(60º + 36º) = 228º — не соблюдается сумма углов треугольника 180º — вариант не верен;
в) при ∠AСB=18º -> 18º + 2(60º + 18º) = 174º — не соблюдается сумма углов треугольника 180º — вариант не верен;г) при ∠AСB=30º -> 30º + 2(60º + 30º) = 210º — не соблюдается сумма углов треугольника 180º — вариант не верен;
д) при ∠AСB=20º -> 20º + 2(60º + 20º) = 180º — соблюдается сумма углов треугольника 180º — вариант верен;