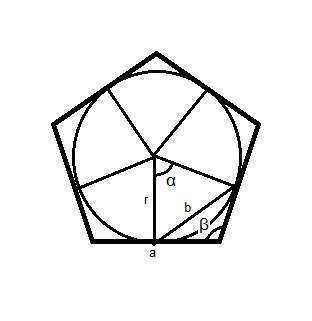
Рассмотрим правильный многоугольник. Я нарисовал 5-угольник для примера.
Проведем радиусы вписанной окружности r и хорду b между ними.
Угол α = 360/n, угол β = 180 - α = 180 - 360/n
По формулам приведения cos (180 - α) = -cos α
По теореме косинусов
b^2 = r^2 + r^2 - 2r*r*cos α = 2r^2*(1 - cos(360/n))
b^2 = (a/2)^2 + (a/2)^2 - 2*a/2*a/2*cos β = 2(a/2)^2*(1 + cos(360/n))
Приравниваем правые части этих формул
2r^2*(1 - cos(360/n)) = 2(a/2)^2*(1 + cos(360/n))
Кроме того, по условию a/r = 2; то есть a/2 = r. Получаем
2r^2*(1 - cos(360/n)) = 2r^2*(1 + cos(360/n))
1 - cos(360/n) = 1 + cos(360/n)
cos(360/n) = 0
360/n = 90
n = 4
Ответ: это квадрат.