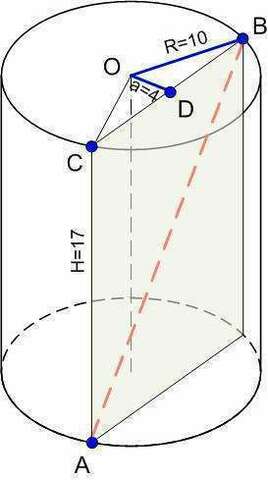
Возьмем точку А на окружности нижнего основания цилиндра и точку B на окружности верхнего основания цилиндра. Соединим эти точки, получая прямую AB, длину которой требуется найти. Спроецируем точку А на верхнее основание цилиндра, получая точку С. Точки А, В, С однозначно определяют плоскость, в которой будет лежать прямая АВ. Расстояние от оси цилиндра, проходящей через центры его оснований до этой плоскости по условию равно 4. Чтобы показать это расстояние, опустим из точки О - центра окружности верхнего основания цилиндра, - перпендикуляр на хорду ВС, получая точку D. Длина отрезка OD равна 4. Обозначим OD через a, тогда a=4. Радиус окружностей в основаниях цилиндра, показанный отрезком OB обозначим через R. По условию R=10. Также, в условии дана высота цилиндра АС, которую обозначим через Н=17.
Рассматриваем ΔDOB. Он прямоугольный, потому что OD⊥DB (по построению). По теореме Пифагора определим катет DB.
DB = √(R² - a²) = √(10² - 4²) = √(100 - 16) = √84 = 2√21
Теперь рассмотрим ΔАСВ. Он также прямоугольный, поскольку образующие цилиндра (АС - одна из образующих) перпендикулярны плоскостям его оснований (ОС лежит в плоскости верхнего основания цилиндра).
ΔCOD = ΔDOB (по двум сторонам и углу). Длина катета ВС равна удвоенной длине DB, т.е. 2 х 2√21 = 4√21, а длина второго катета известна: Н=17.
Находим гипотенузу АВ по теореме Пифагора.
AB = √(BC² + AC²) =√(16 x 21 + 17²) = √(336 + 289) = √625 = 25
Ответ: 25