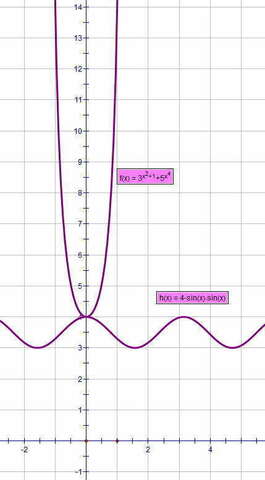
Здесь только рассуждать о свойствах функций...
в показателях степени выражения неотрицательные, т.е. наименьшие значения для показателей степени ---это нули,
а чем больше показатель степени,
тем больше значение ф-ции (основания >1), значит слева от равенства
меньшее значение (при х=0) 3^1 + 5^0 = 3+1 = 4
синус ф-ция периодическая и ограниченная, хоть в какую степень ее возводи ---больше 1 она не будет)))
-1 < sin(x) < 1
0 < (sin(x))² < 1
0 > -(sin(x))² > -1
-1 < -(sin(x))² < 0
4-1 < 4-(sin(x))² < 4
т.е. эти функции "встретиться" могут только в одной точке... при х = 0
это и есть единственное решение...