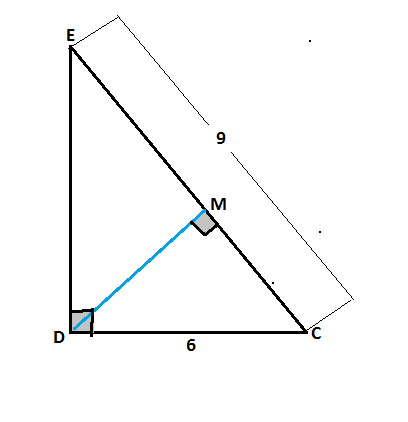
Найти СМ можно несколькими способами.
1)
Через подобие треугольников СDЕ и СDМ, т.к. высота прямоугольного треугольника делит его на подобные треугольники.
Тогда ЕС:DС=DС:СМ
DС²=ЕС*СМ
36=9 СМ
СМ=36:9=4 см
-----------
2)
По свойству катета прямоугольного треугольника:
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
СМ- проекция катета СD на гипотенузу. Отсюда
СD²=МС*ЕС
36=9*МС
МС=36:9=4 см
3)
Из площади треугольника СDЕ. Это решение значительно длиннее первых двух, но, возможно, Вы еще не проходили подобие фигур.
S =DЕ*СD
По т.Пифагора
DЕ-√(СЕ²-СD²)=√45=3√5
Тогда
Ѕ=(6*3√5):2=9√5
Тогда высота треугольника DСЕ
DМ=2 Ѕ:ЕС:ЕС
DМ=(18√5):9=2√5
Из прямоугольного треугольника СДЕ катет
СМ по т. Пифагора
МС=√(СD²-DМ²)
МС=√(36-20)=4 см