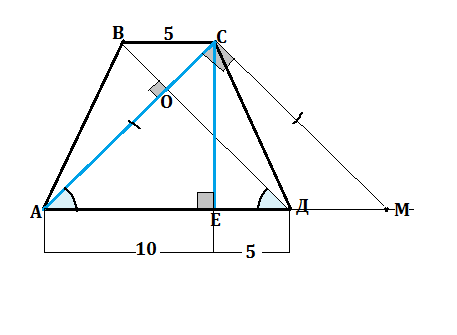
В равнобедренной трапеции длины диагоналей равны. ( свойство)
Высота равнобедренной трапеции, опущенная из тупого угла, делит основание на отрезки, больший из которых равен полусумме оснований.
АЕ=(ВС+АЛ):2=(5+15):2=10
Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
СЕ=АЕ=10
Подробнее:
Проведем СМ || ВД.
СМ=ВД=АС⇒ АСМД - параллелограмм, ДМ=ВС, АМ=АВ+ВС=20
∆ АСМ - равнобедренный прямоугольный.
Углы при основании равнобедренного прямоугольного треугольника равны 45°
Треугольники АСЕ и МСЕ- прямоугольные.
Угол АСЕ=90°-45°=45°
Угол МСЕ=90°-45°=45°⇒
СЕ- биссектриса и медиана
Медиана прямоугольного треугольника равна половине гипотенузы.
СЕ=АЕ=АМ*2=
10
Тот же результат получим, если будем из треугольника АСЕ по т.Пифагора находить СЕ.