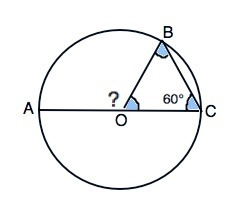
Угол СОВ - вписанный. Угол АОВ – центральный и опирается на ту же дугу.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу. ⇒ угол АОВ=2•60°=120°.
Вариант решения.
В ∆ ВОС стороны ВО=СО - радиусы.
ВС=R ( дано)⇒
∆ ВОС - равносторонний.
АС - диаметр,⇒ угол АОС - развёрнутый.
Смежный с углом ВОС угол АОВ=180°-60°=120°