Нужна помощь! 1.Найти область определения 2. определить, четная или не четная...

№ 1.
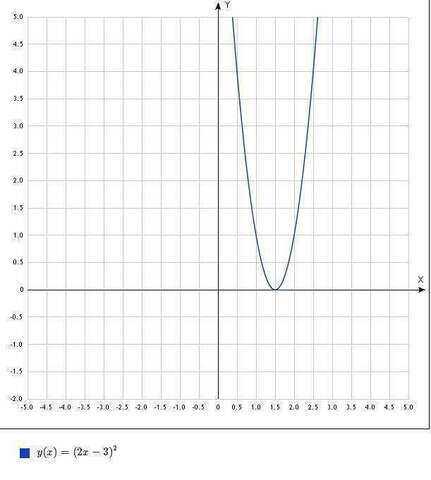
D(y)=(-∞;+∞)
y(-x)=(-2x-3)²=(2x+3)² - функция не является ни четной, ни нечетной.

№ 2.
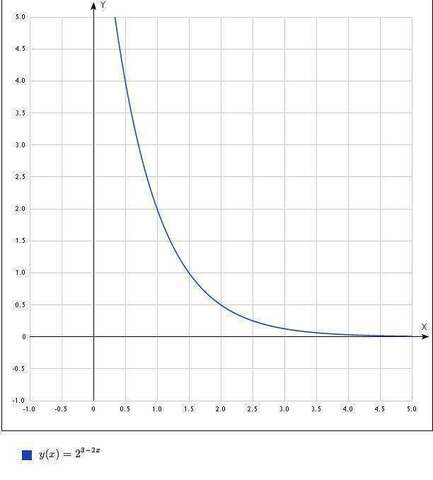
D(y)=(-∞;+∞)
$y(-x)=2^{3+2x}$ - функция не является ни четной, ни нечетной.

№ 3.
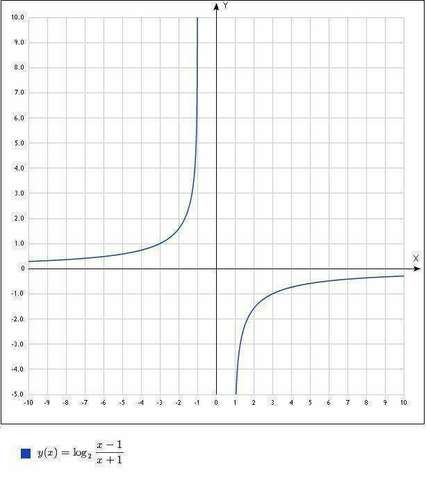
D(y)=(-∞;-1)U(1;+∞)
$\frac{x-1}{x+1}\ \textgreater \ 0$

___+_____(-1)_____-_______(1)_______+________ x

$y(-x)=log_{2} \frac{-x-1}{-x+1}=log_{2}\frac{x+1}{x-1}=log_{2}(\frac{x-1}{x+1})^{-1}=-log_{2}\frac{x-1}{x+1}=-y(x)$ - функция нечетная.

№ 4.
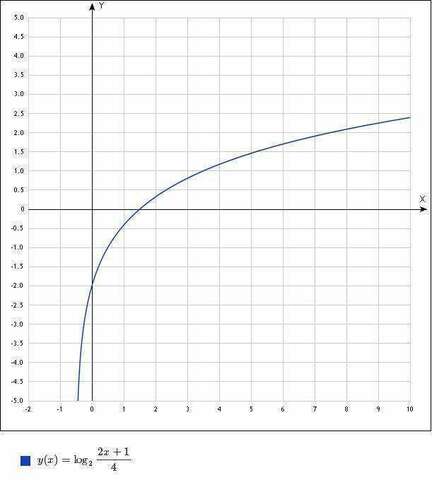
D(y)=(-0.5;+∞)
$\frac{2x+1}{4}\ \textgreater \ 0$
$2x+1\ \textgreater \ 0$
$x\ \textgreater \ -0.5$
$y(-x)=log_{2} \frac{-2x+1}{4}$ - функция не является ни четной, ни нечетной.

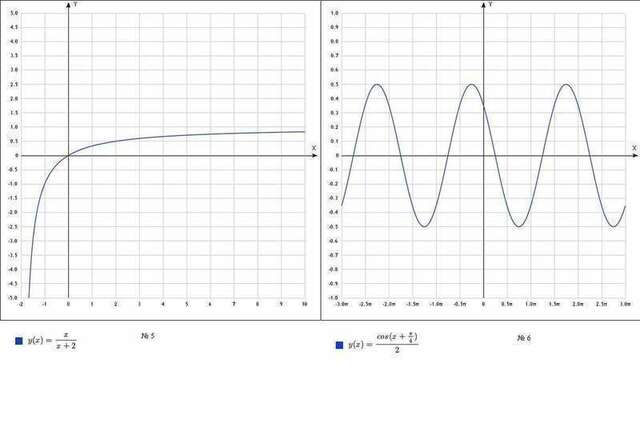
№ 5.
D(y)=(-∞;-2)U(-2;+∞)
$x+2 \neq 0$
$x \neq -2$
$y(-x)= \frac{-x}{-x+2}=\frac{x}{x-2}$ - функция не является ни четной, ни нечетной.

№ 6.
D(y)=(-∞;+∞)
$y(-x)=0.5*cos(-x+ \frac{ \pi }{4})=0.5*cos(x- \frac{ \pi }{4})$ - функция не является ни четной, ни нечетной.

ГРАФИКИ ПРИКРЕПЛЕНЫ