Окружность прохордит через вершины a,b,d трапеции ABCD. AD- Большее основание и касается...

Question

Дано ответов: 2

Правильный ответ

ВС=СD=5, как касательные из одной точки.
ВЕ - перпендикуляр в точку касания и делит AD пополам (свойство).
Опустим перпендикуляр СН из точки С на AD.
Тогда СН=ВЕ. Из прямоугольного треугольника НСD по Пифагору CН²=CD²-HD².
Из прямоугольного треугольника ВЕD по Пифагору ВЕ²=ВD²-ЕD². Итак, CD²-HD²=ВD²-ЕD².
Пусть ED = Х. Тогда HD=Х-5 (так как ЕН=ВС=5).
Имеем уравнение: CD²-HD²=ВD²-ЕD² или
5²-(Х-5 )²=8²-Х² или 25-Х²+10Х-25=64-Х² или 10Х=64. Отсюда Х=6,4.
Тогда CD=2Х = 12,8.
Ответ: CD=12,8.

Andr1806_zn (117k баллов) 11 Апр, 18

nafanya2014_zn · Answer 1 · 2018-04-11T11:02:26+0000

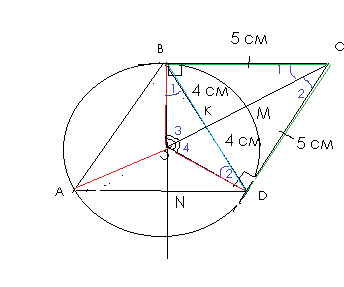
ВС и СD- касательные, проведенные из точки С
Отрезки касательных, проведенных из одной точки, равны.
ВС=CD=5
Треугольник ВСD - равнобедренный. Высота СК является и медианой.
ВК=KD= 4
и биссектрисой ∠1=∠2
sin ∠1=4/5=0,8

Значит и вторые острые углы прямоугольных треугольников ОВС и ОВD равны между собой:∠3=∠4

Треугольник BOD - равнобедренный
∠3=∠4 значит и вторые углы равны, обозначим их также ∠1=∠2

BC | | AD
BO ⊥ ВС
значит BO⊥ AD
Продолжим радиус BO до пересечения с AD, получим точку N
Диаметр, перпендикулярный хорде, делит хорду пополам
AN=ND
Из прямоугольного треугольника BND:
ND= BD·sin∠1=8·0,8=6,4 м
AD=2·6,4=12,8 м