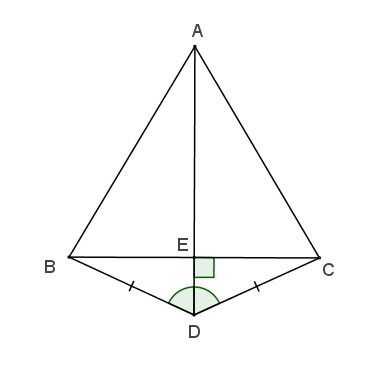
Пусть E - точка пересечения прямых BC и AD. Если Е не совпадает с D (на чертеже изображен как раз один из таких случаев), то прямоугольные треугольники BED и CED равны по гипотенузе и катету:
BD=CD по условию, а ED - общий катет. Отсюда ∠BDE=∠CDE,
а т.к. точки A,D,E лежат на одной прямой, то и ∠BDA=∠CDA.
(Заметим, что если Е совпала с D, то равенство углов ∠BDA и ∠CDA следует сразу из условия, т.к. BC⊥AD).
Далее, треугольники BDA и CDA равны по сторонам и углу между ними
(AD - общая, BD=CD по условию, ∠BDA=∠CDA доказали выше), а значит, AB=AC, что и требовалось.