Сначала лирическое отступление
y(x)=x^2/(x-3) =(x^2-3x+3x-9+9)/(x-3) = x+3 + 9/(x-3)
из полученного выражения уже понятно как выглядит график
это сумма трех функций у=х у=3 у=9/(x-3)
***********************
1)область определения
знаменатель не равен 0 значит х не равен 3
2)четность
y(-x)=x^2/(-x-3)
функция ни четная ни нечетная
3)
из первого пункта - вертикальная асимптота х=3
4)
производная
y` = 1-9/(x-3)^2
5)
экстремумы
производная равна нулю при х1=0 и х2=6
y``=9/2 * 1/(x-3)^3
y`(x1) = -3/2 <0 значит х1 - точка локального максимума<br>y`(x2) = 3/2 >0 значит х2 - точка локального минимума
6) точек перегиба нет так как нет таких точек что y``=9/2 * 1/(x-3)^3 = 0
7) есть наклонная асимптота у = х+3, искать ее надо при помощи
пределов, оставляю это занятие автору вопроса или может посмотреть на
лирическое отступление в начале
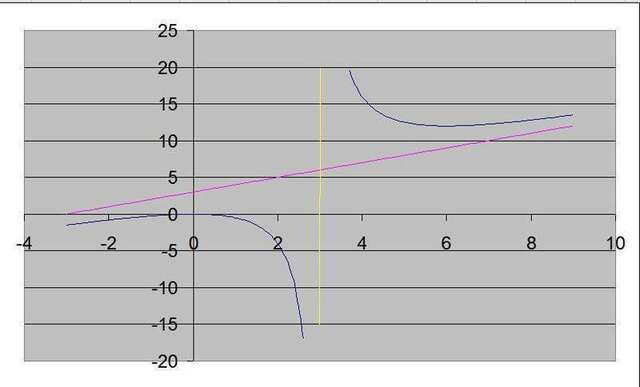
8)график во вложении, на нем отображены вертикальная и наклонная асимптоты