Биссектриса треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
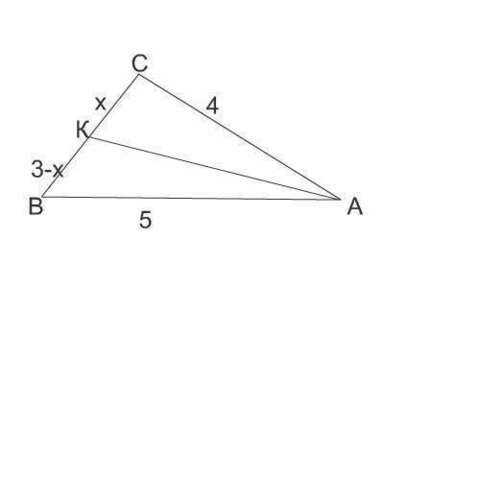
Рассмотрим рисунок. Согласно теореме о биссектрисе угла, составим пропорцию:
АС:СК=АВ:ВК
ВС найдем по теореме Пифагора. Она равна 3. Но этот треугольник -египетский, можно обойтись знанием сторон такого треугольника.
Пусть СК=х, тогда КВ=(3-х)
Вставим известные величины в пропорцию:
4:х=5:(3-х)
5х=12-4х
9х=12
х=12/9=4/3
Биссектрису АК найдем по т. Пифагора:
АК²=АС²+КС²=16+16/9=160/9
АК=√160/9=(4√10):3