1)
средняя линия трапеции равна полусумме оснований ⇒
пусть неизвестное основание x, тогда
16=(12+x)/2
12+x=32
x=20 - второе основание
2)
первое основание 5x
второе основание 7x
тогда (5x+7x)/2=36
12x/2=36
6x=36
x=6
первое основание равно 5*6=30
второе 7*6=42
3)
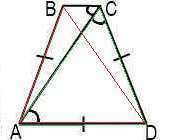
пусть дана трапеция АВСД, где АД - большее основание, ВС - меньшее основание
проведем диагональ АС
отрезки, на которые разделит диагональ среднюю линию будут являться средними линиями для ΔАВС и ΔАСД ⇒
ВС=7*2=14
АД=9*2=18
т.к. диагональ ВД будет биссектрисой тупого угла В , то сторона АВ=АД,
а т.к. диагональ СА будет биссектрисой тупого угла С , то сторона СД=АД
получаем АВ=АД=СД=18
Р(АВСД)=14+18+18+18=68