Условие:
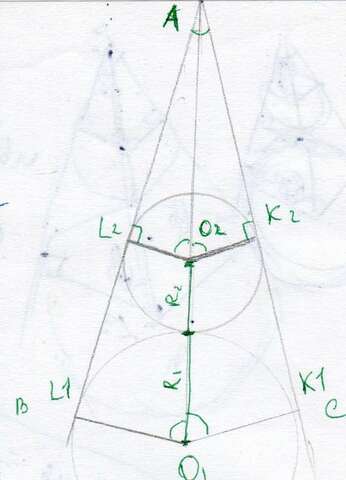
угол ABC
малая окружность(О2;R2)
большая окружность(O1;R1=23)
Решение:
По свойству секущей, угол BL2O2 равен углу ВК2О2, углу ВL1О1 и углу ВК1О1 и равен 90 градусам.
Из четырехугольников L1BK1O1 и L2BK2O2 углы L1O1K1 и L2O2K2 равны 120 градусам из следующего уравнения: 360-2*90-60=120.
Проведем бис-су ВО, которая пересечет центры окружностей О1 и О2.
По свойству катета, лежащего против угла в 30 градусов, гипотенуза прямоугольного треугольника О1В равна двум катетам или радиусам большой окружности и равна 46.
Из прямоугольного треугольника К2О2В гипотенуза О2В равна двум катетам К2О, как и в случае с треугольником К1О1В.
Точка D общая для обеих окружностей.
O1D=R1=23.
O1B=O1D+DB
DB=R1+O2B.
O1B=R1+R2+O2B
O1B=R1+R2+2R2
3R2=O1B-R1
R2=(O1B-R1)/3
Подставим значения:
R2=(46-23)/3
R2=23/3.
Найдем расстояние от точек касания окружностей до вершины угла:
По синусу угла ВО1К1 К1В =(корень из 3)/2*46=23*(корень из 3)
По синусу угла ВО2К2 К2В =(корень из 3)/2*23=11,5*(корень из 3).