А) вводим функцию: у = 3х^2 - 2x - 5
приравниваем к 0: 3x^2-2x-5 = 0
Дискриминант: 4 + 60 = 64
х = 4 плюс минус 8 все делить на 6
х1 = 2, х2 = -2/3
Ответ: х принадлежит (2; + бесконечность)
б) вводим функцию, у = x^2 + 6x + 9
уравнение: x^2 + 6х + 9 = 0
Дискриминант: 36-36=0
х = -6 плюч минус 0 все делить на 2
х = -3
Ответ: х принадлежит (- бесконечноть; -3)
в) Используем метод интервалов.
(х-3)(х+5) > 0
х = 3, х = -5 .
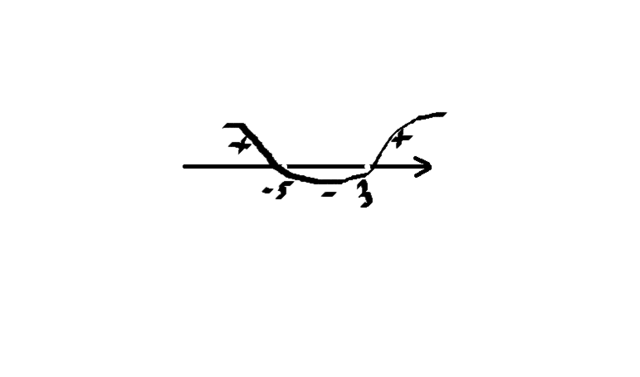
Чертим прямую координат, она будет в приложении.
Отмечаем точки, находим промежутки. Точки на координатах проколотые, то есть не надо их закрашивать.
Подставляем в промежутки числа.
х от 0 = (0-3)(0+5) = -3*5= отрицательное число, ставим минус.
х от 10 = (10-3)(10+5) = положительное число, +
х от -10 = (-10-3)(-10+5) = минус на минус дает плюс = +
Ответ: х принадлежит (- бесконечности; -5)V(3; + бесконечности)