1)
Общей частью двух конусов, расположенных подобным образом, будет тело вращения, состоящее из двух одинаковых конусов, прилегающих друг к другу основаниями.
Рассмотрим осевое сечение образовавшегося тела (см. рис. 1).
Δ DBE ~ Δ ABC по двум углам с коэффициентом подобия 1/2. Этот вывод следует из соображений симметрии: образующие одинаковых конусов пересекаются на высоте, равной половине высоты конуса.
Объёмы подобных тел относятся как куб коэффициента подобия, т. е. объём «малого» конуса, представленного на рисунке треугольником DBE, равен: (1/2)³∙V = V/8.
Окончательно, объём общей части двух конусов равен: 2∙V/8 = V/4.
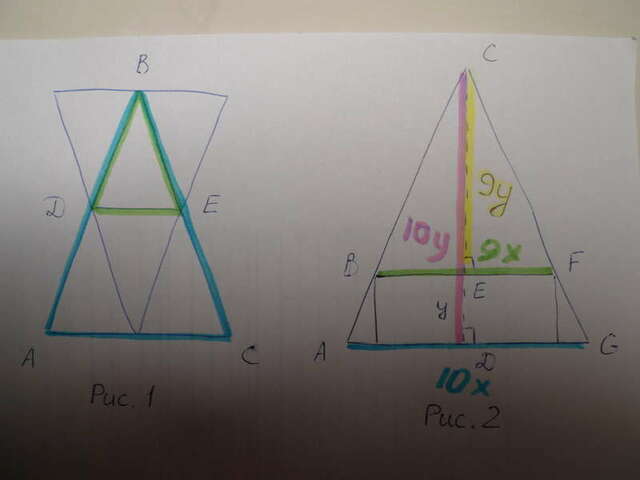
2) Рассмотрим осевое сечение образовавшегося тела (см. рис. 2).
Δ BCF ~ Δ ACG по двум углам. У подобных треугольников отношение любых соответствующих линейных размеров одинаковы.
Т. е. CE/CD = BF/AG = 9/10.
Откуда CE = 9/10 CD. Следовательно, ED = CD – CE = 1/10 CD.
Обозначим диаметр конуса как 10x, тогда диаметр цилиндра будет 9x.
Обозначим высоту конуса как 10y, тогда высота цилиндра будет y.
Объём конуса равен: V = 1/3∙π∙(10x/2)²∙10y = 250/3∙πx²y. Откуда: πx²y = 3/250∙V.
Объём цилиндра равен: π∙(9x/2)²∙y = 81/4∙πx²y = 81/4∙3/250∙V = 243/1000∙V = 0,243V