Решите неравенство -18/(х+4)^2-10》0

$- \frac{18}{(x+4)^2}-10 \geq 0$
$\frac{-18-10*(x+4)^2}{(x+4)^2} \geq 0$
$-18-10*(x+4)^2\geq 0$
$-18-10*(x^2+8x+16)\geq 0$
$-18-10x^2-80x-160\geq 0$
$-10x^2-80x-178\geq0|:2$
$-5x^2-40x-89\geq 0$

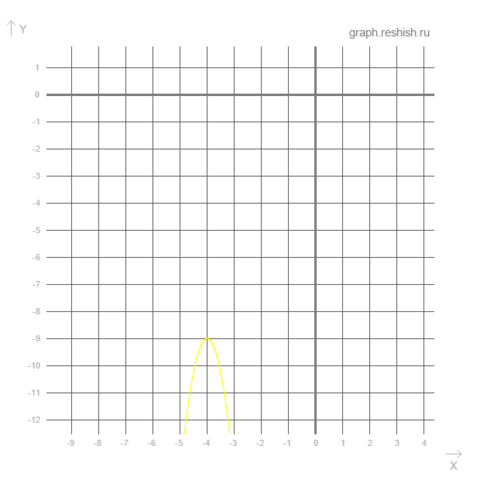
Квадратное уравнение:
$-5x^2-40x-89=0$
a=-5 - старший коэффициент при x^2;
b=-40 - второй коэффициент при x;
c=-89 - свободный член.
График функции - парабола с ветвями вниз, так как значение "a" при старшем коэффициенте $x^2$ меньше нуля.
Вычислим дискриминант:
$D=b^2-4*a*c$
$D=(-40)^2-4*(-5)*(-89)=1600-1780=-180$
Ответ: Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.

Корни квадратного уравнения - точки пересечения с осью абсцисс x. Построение графика функции подтверждает ответ - отсутствие точек пересечения с осью x.