Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
d₁²+d₂²=a²+b²+a²+b²
13²+15²=2·(a²+b²)
169+225=2·(a²+b²)
197=a²+b²
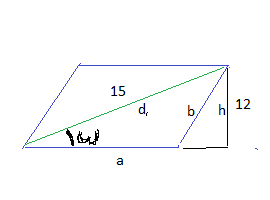
Cм. рисунок в приложении
sin ω=12/15=4/5
cosω=3/5
так как sin²ω+cos²ω=1
По теореме косинусов
b²=a²+15²-2a·15 cosω
b²=225+a²-18a
Так как a²+b²=197, то заменяя b² на 225+а²-18а, получим уравнение
а²+225+а²-18а=197
2а²-18а+28=0
а²-9а+14=0
D=81-56=25
a₁=(9-5)/2=2 или а₂=(9+5)/2=7
b₁=√193 или b₂=√148