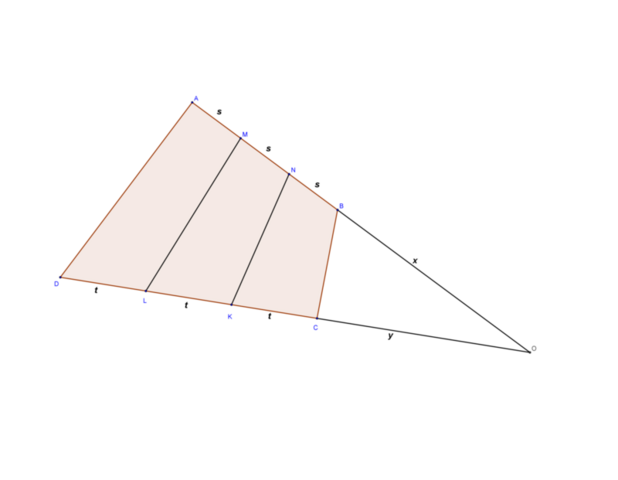
Пусть продолжения прямых AB и CD за точки B и С пересекаются в О и пусть OB=x, OC=y, AM=MN=NB=s, DL=KL=KC=t. Тогда
S(ABCD)=S(OAD)-S(OBC)=1/2*((x+3s)*(y+3t)-xy)*sin(∠BOC)
S(KLMN)=S(OML)-S(ONK)=1/2*((x+2s)*(y+2t)-(x+s)(y+t))*sin(∠BOC)
Отсюда S(ABCD)/S(KLMN)=(3sy+3xt+9st)/(2sy+2xt+4st-sy-xt-st)=3.