ПОМОГИТЕ! ЗАДАЧА. РЕШИТЕ ПОЖАЛУЙСТА СО ВСЕМИ ДАНО, НАЙТИ И РЕШЕНИЕМ. И ЧЕРТЕЖ.

S(бок)=π(r₁+r₂)·l

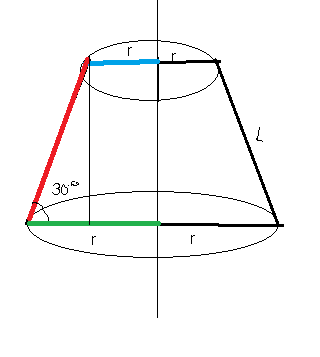
Осевое сечение представляет из себя трапецию
Верхнее основание равно 2r₁
Нижнее основание 2r₂
Проведем высоту трапеции из вершины меньшего основания опустим перпендикуляр на нижнее. Получим прямоугольный треугольник с острым углом 30°
Катет против угла в 30° равен половине гипотенузы. поэтому высота трапеции равна l/2

По формуле площади трапеции

$F= \frac{2r_1+2r_2}{2}\cdot \frac{l}{2} \Rightarrow 2F=(r_1+r_2)\cdot l$

S(бок)=π(r₁+r₂)·l=2π·F

Ответ. 2π·F