1)
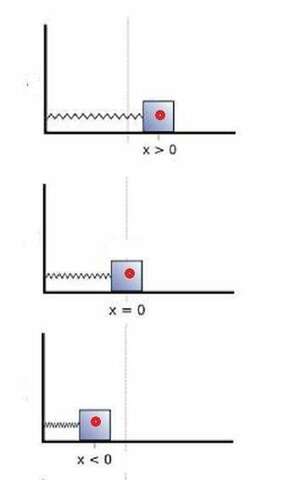
Рассмотрим положение тела на первом рисунке (груз в правом крайнем положении).
Запишем уравнение движения в виде:
x (t)= Xmax* sin *(2π*t /T + π/2) (это тоже уравнение гармонического колебания начальной фазой).
Если (t = 0) то x(0) = Xmax
Скорость движения груза - первая производная от x:
v(t) = (x(t))' = (2π*A/T)*cos ((2π/T) *t + π/2) = Vmax* cos ((2π/T) *t + π/2)
Если (t = 0) то v(0) = 0 (тело остановится)
И, наконец, аналогично находим ускорение тела:
a (t)= (x''(t)) = (v'(t)) = - Amax sin ((2π/T) *t + π/2 )
Если (t = 0) то a(0) = - Amax (направление вектора ускорения сменилось на противоположное, сила направлена к положению равновесия)
2)
Рассмотрим положение тела на втором рисунке (груз в положении равновесия).
Если (t = T/4) то:
x(T/4) = 0 (тело в положении равновесия).
v(T/4) = - Vmax (тело проходит положение равновесия с максимальной скоростью.
a(T/4)= 0 (равнодействующая сил равна нулю (пружина не растянута).
Выбираем ответы:
Б) и Г)