Длины катетов прямоугольного треугольника АВС равны 6см и 4см. Больший катет АС разделен...

Question

Длины катетов прямоугольного треугольника АВС равны 6см и 4см. Больший катет АС разделен точками М и N на 3 равны части. точки М и N соединены вершиной В. найди площадь треугольника ВМN.

Answer 1

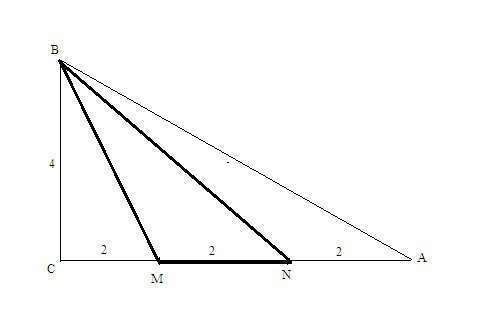
Вот рисунок.
MN = 2; MB = √(4^2 + 2^2) = √(16 + 4) = √20 = 2√5
NB = √(4^2 + 4^2) = √(16 + 16) = √32 = 4√2
По формуле Герона
p = (MN + NB + MB)/2 = (2 + 2√5 + 4√2)/2 = 1 + √5 + 2√2
S^2 = p(p - MN)(p - MB)(p - NB) =
= (1 + √5 + 2√2)(√5 + 2√2 - 1)(1 - √5 + 2√2)(1 + √5 - 2√2) =
= [((√5+2√2) + 1)((√5+2√2) - 1)]*[(1 - √5 + 2√2)(1 + √5 - 2√2)] =
= [(√5+2√2)^2 - 1]*[1-√5+2√2+√5+2√10-2√2+2√10-8] =
= (5 + 8 + 4√10 - 1)*(4√10 - 7) = (4√10 + 12)(4√10 - 7) =
= 16*10 + 48√10 - 28√10 - 84 = 76 + 20√10
S = √(76 + 20√10) ~ 11,8 кв.см.

---