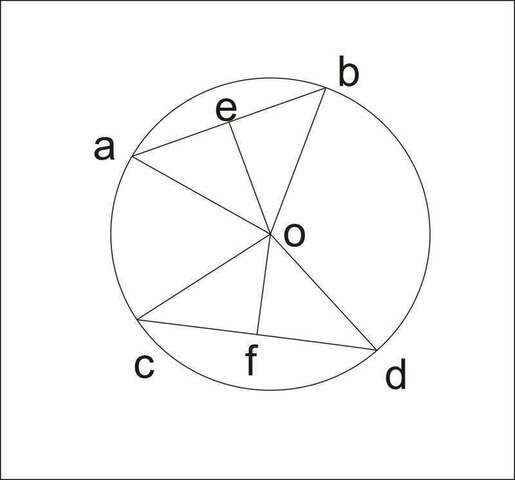
Построим окружность с центром в точке о и проведем хорды АВ и
СД удовлетворяющие условиям задачи.
Найдем радиус данной окружности:
Построим радиусы ОА и ОВ, а также ОЕ- расстояние от центра
окружности до хорды АВ (ОЕ ⊥ АВ)
Рассмотрим получившийся треугольник ОАВ – равнобедренный,
так как ОА=ОВ (радиусы окружности).
Так как ОАВ равнобедренный, то ОЕ - является и высотой и медианой.
Значит АЕ=АВ/2=40/2=20
Рассмотрим треугольник ОАЕ: угол ОЕА – прямой.
По теореме Пифагора найдем ОА:
ОА= √(АЕ^2+OE^2)=
√(20^2+21^2)= √(400+441)= √841=29 – Мы нашли радиус окружности.
Теперь находим расстояние от центра окружности до хорды СД:
Построим радиусы ОС и ОД, а также ОF- расстояние от центра окружности до хорды
СД (ОF ⊥ СД)
Рассмотрим получившийся треугольник ОСД – равнобедренный, так
как ОС=ОД (радиусы окружности).
Так как ОCД равнобедренный, то ОF - является и высотой и медианой.
Значит СF=СД/2=42/2=21
Рассмотрим треугольник ОCF: угол ОFC – прямой.
По теореме Пифагора найдем ОF:
OF=√(OC^2-CF^2)= √(29^2-21^2)= √(841-441)= √400=20
Ответ: расстояние от центра окружности до хорды СД равно 20