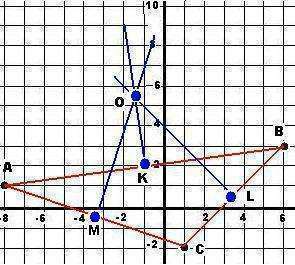
Центр окружности находим как показано на рисунке - точка пересечения прямых из середин сторон треугольника.
Для стороны АВ.
Уравнение прямой АВ k1 = (Ву-Ау)/(Вх-Ах) = 2/14 = 1/7.
3= 1/7*6 + b или b1 = 3-6/7 = 2 1/7 и уравнение у1 = 1/7*х +2 1/7
Координаты точки К
Кх= -1, Ку = 2 1/7 - 1/7 = 2. Точка К(-1;2).
Уравнение перпендикуляра - прямой ОК.
к2 = -1/к1 = 7. для точки К 2 = 7*(-1)+b2 и b2= -5.
Окончательно у2 = -7*х-5.
Для прямой ВС уравнение у3= х-3
Координаты точки L. Lx=3.5 и Lу=0,5. Окончательно L(3.5;0.5).
Уравнение перпендикуляра - прямой OL.
к4 = -1/к3 =-1. Для точки L - 0.5 = -3.5+b4 и у4= -х+4.
И центр окружности - точка пересечения перпендикуляров. Решаем систему уравнений для прямых у2 и у4.
-7*x-5 = -x+4 или 6*х= -9 или для точки О Ох= 1,5 - ОТВЕТ
Оу= -х+4 = 5,5 - ОТВЕТ.
Окончательно: О(-1,5; 5,5)