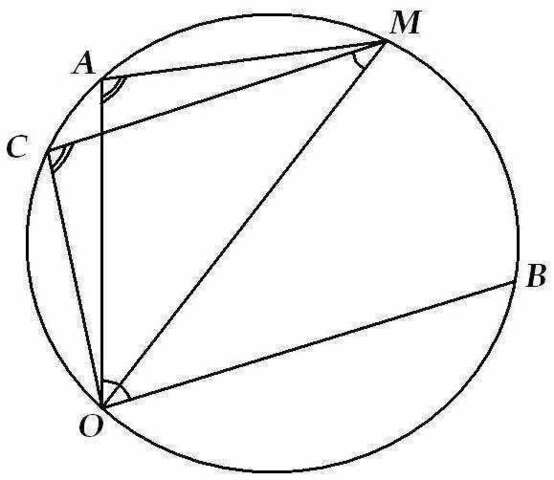
Смотрим картинго:
окружность, вписанный угол АОВ, ОМ - биссектриса, МС || ОВ
Нужно доказать, что МС=ОА
∠СМО=∠ВОМ, как накрест лежащие при пересечении параллельных прямых секущей, значит ∠СМО=∠АОМ, т.к. ОМ - биссектриса.
∠ОСМ=∠МАО, как опирающиеся на одну и ту же дугу ОВМ.
Таким образом в ΔОСМ и ΔМАО ∠СОМ=∠АМО, так как два других угла
ΔОСМ равны двум другим углам ΔМАО. ОМ - общая сторона этих Δ-ков,
значит ΔОСМ=ΔМАО по второму признаку равенства Δ-ков и МС=ОА
ЧТД