Окружность, вписанная в равнобокую трапецию ABCD , касается основания AD в точке N , а...

Question

Окружность, вписанная в равнобокую трапецию ABCD , касается основания AD в точке N , а боковой стороны AB в точке M. Диагональ AC пересекает отрезок MN в
точке K NK=2MK , BC = 2. Найти радиус окружности

Comments

Можешь рисунок нарисовать пж я

---

Собственно не понятно, за что тут 50 баллов. АМ=AN как отрезки касательных, AK - медиана равнобедренного треугольника, значит она его биссектриса. Т.е. центр окр. лежит на AC В силу симметрии и на BD. Т.е. диагонали пересекаются в центре этой окружности, Значит BC=AD, значит наша трапеция - квадрат. Значит радиус равен 2.

---

Вернее это диаметр равен 2, а радиус равен 1.

---

извиняюсь пропустил в условии 2

---

Теперь другое дело.

Answer 1

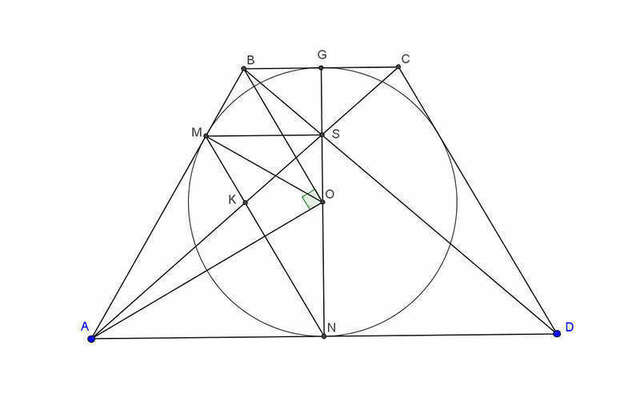
Пусть вписанная окружность имеет центр О и касается основания BC в точке G и пусть S - точка пересечения диагоналей трапеции. Тогда BM/AM=BG/AN=BS/DS. Значит треугольники MBS и ABD подобны, т.е. MS||AD. Отсюда треугольники MKS и NKA подобны, а значит AN/MS=NK/MK=2. Дальше AB/MB=AD/MS=2AN/MS=4, откуда AB=4, AM=4-1=3 потому что MB=1. И т.к. треугольник AOB - прямоугольный (AO и BO - биссектрисы углов, сумма которых 180), то радиус OM - его высота, т.е. OM=√(MB·AM)=√(1·3)=√3.

---