Тригонометрические неравенства. Прошу модераторов не удалять ** какое-то время.

Question

Дан 1 ответ

Правильный ответ

$sinx(sinx-\frac{1}{2})\ \textless \ 0\; \; \Rightarrow \; \; 0\ \textless \ sinx\ \textless \ \frac{1}{2}\; \; \Leftrightarrow \left \{ {{sinx\ \textgreater \ 0} \atop {sinx\ \textless \ \frac{1}{2}}} \right. \\\\ \left \{ {{2\pi n\ \textless \ x\ \textless \ \pi +2\pi n,n\in Z} \atop {-\frac{7\pi}{6}+2\pi k\ \textless \ x\ \textless \ \frac{\pi}{6}+2\pi k,k\in Z}} \right. \; \Rightarrow \\\\x\in (-\frac{7\pi}{6}+2\pi n;-\pi +2\pi n )\cup (2\pi n;\frac{\pi}{6}+2\pi n)\; \; ili\\\\x\in (2\pi n;\frac{\pi}{6} +2\pi n)\cup (\frac{5\pi}{6}+2\pi n;\pi+2\pi n)$

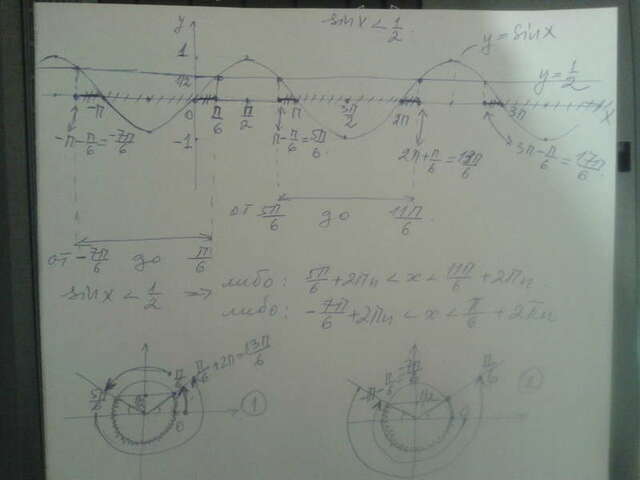
Отметим решения неравенства $sinx\ \textless \ \frac{1}{2}$ на триг. круге.Область лежит ниже прямой у=1/2. Точки пересечения мы видим такие:

$x=\frac{\pi}{6} \; ,x=\pi -\frac{\pi}{6}=\frac{5\pi}{6}$

Но нам нужы углы, лежащие ниже указанных, причём
двигаться должны от меньшего к большему, а значит
начинать с угла х=П/6 нельзя. Поэтому, если начальный
угол будет х=5П/6, то за ним мы пойдём к углу 2П+П/6=13П/6.
Понятно, что нужно будет прибавить период 2Пn.
Решение можно записать в виде:

$\frac{5\pi}{6}+2\pi n\ \textless \ x\ \textless \ \frac{13\pi }{6}+2\pi n,\; n\in Z$

Но всегда лучше брать интервалы более близкие к 0.
Поэтому можно до точки, соответствующей углу 5П/6
пойти в отрицательном направлении по часовой стрелке,
тогда соответствующий угол будет равен -П-П/6=-7П/6.
А затем от этого угла будем уже двигаться ко второму углу
по часовой стрелке в положительном направлении.
Мы дойдём до начала отсчёта ( до нуля), а потом
уже продвинемся до угла П/6. Опять надо будет прибывить период
и получим такую серию решений:

$-\frac{7\pi}{6}+2\pi n\ \textless \ x\ \textless \ \frac{\pi}{6}+2\pi n,\; n\in Z$

Ещё можно построить графики .См. вложение.

NNNLLL54_zn (832k баллов) 13 Апр, 18