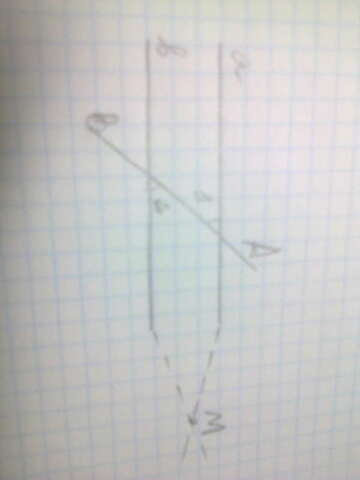
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 1 = ∠ 2. Докажем, что а параллельно b.
Предположим, что прямые а и b не параллельны. Тогда они пересекаются в какой-то точке М ⇒ один из углов 1 или 2 будет внешним углом Δ АВМ. Пусть для определенности ∠ 1 — внешний угол Δ АВМ, а ∠ 2 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 1 больше ∠ 2, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.