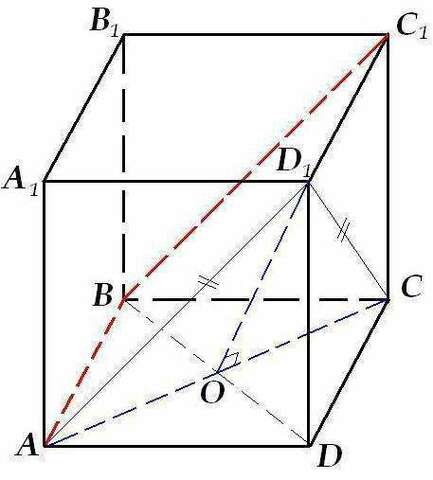
1) Возможно, тут и как-то по-другому нужно доказывать, но так тоже всё верно:

, как диагoнали равных квадратов, значит Δ

- равнобедренный, О - середина АС, значит

- медиана, биссектриса и высота, то есть

⊥
 ЧТД
2)
ЧТД
2) Можно по достаточному условию перпендикулярности прямой и плоскости:
Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

⊥

,

⊥

, значит

⊥

, и перпендикулярна любой прямой этой плоскости, в том числе

, значит ∠
 ЧТД
ЧТД
Можно по теореме о трёх перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и самой наклонной.
Здесь ещё проще: АВ проведена через основание наклонной

,

- проекция

на плоскость АВС и

⊥

, значит

⊥

и ∠
 ЧТД
ЧТД