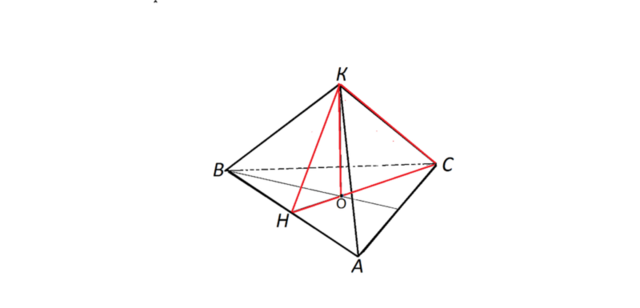
Боковое ребро правильной треугольной пирамиды равно 5см, а высота -корень из 13. Найти площадь боковой поверхности пирамиды.
Площадь боковой поверхности правильной пирамиды равна сумме площадей ее боковых граней, равных между собой.
Площадь одной боковой грани - площадь равнобедренного треугольника,
т.е. половина произведения апофемы на сторону основания пирамиды.
См. рисунок:
S бок= 3 SᐃAKB= 3 KH*AB:2
Основание О высоты КО правильной пирамиды находится в точке пересечения высот её основания ( центре вписанной окружности).
Этот центр делит высоту основания СН в отношении 2:1, считая от вершины треугольника ( по свойству медиан, которые в правильном треугольнике и высоты, и биссектрисы).
Итак, ОН=ОС:2.
ОС=√(КС²-ОК²)=√(25-13)=2√3 см
ОН=√3 см
Апофема
КН=√(КО²+ОН²)=√(13+3)=4 см
АВ=АС=ВС=СН:sin(60°)
СН=ОН+ОС=3√3
АВ=2*(3√3):√3=6 см
S бок=0,5*KH*AB=2*3*6=36 см²