острый угол ромба 60 градусов, а его площадь 54корнеь3.Найти длину большей диагонали ромба

1. Площадь ромба

за формулой $S=a^2sin\alpha,$ где $\alpha$ - острый угол между сторонами ромба, найдем его сторону:

54 $54\sqrt3=a^2sin60\\$

$a^2=\frac{54\sqrt3}{sin60}\\$

$a^2=\frac{54\sqrt3}{\frac{\sqrt3}{2}}={54\sqrt3}\cdot\frac{2}{\sqrt3}=54*2=108$

$a=\sqrt{108}=4\sqrt7$

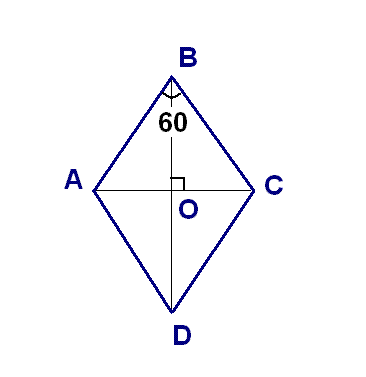
2.Диагонали ромба пересекаются под прямым углом, значит угол АОВ = 90 градусов.

диагонали ромба также являются его бисектрисами.

т.о. угол АВО=30.

значит треугольник АОВ - прямоугольный (угол АОВ=90) с острым углом АВО = 30.

и что следует с п.1 стороной а= $4\sqrt7$ .

3. $cosABO=\frac{BO}{AB}$

$BO=AB\cdot cos{ABO}$ $BO=4\sqrt7 \cdot cos30 = 4\sqrt7 \cdot \frac{\sqrt3}{2}=2 \cdot \sqrt{21}$

BD=2*BO

BD=2* $BD=2\cdot BO= 2 \cdot 2 \sqrt{21} = 4 \sqrt{21}$