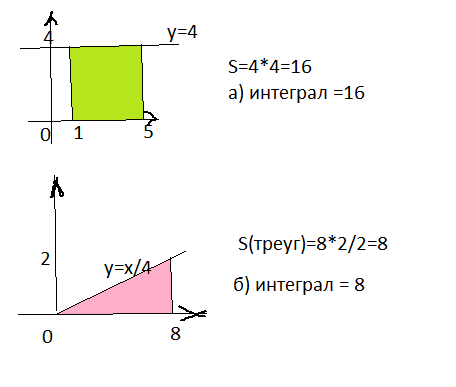Геометрический смысл интеграла, площадь фигуры под кривой (прямой), заданной на отрезке [a;b]
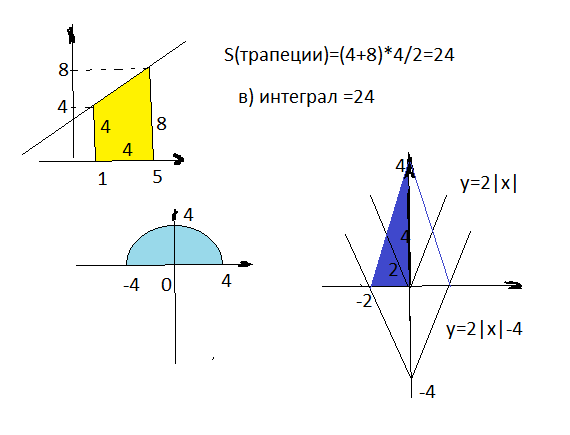
2а) В пределах интегрирования опечатка должно быть от -4 до4
у=√16-х²- уравнение полуокружности с центром в точке (0;0) радиусом 4
у²=16-х² или х²+у²=16
Интеграл равен площади половины круга ( в верхней полуплоскости)
Ответ π4²/2=8π
2б) площадь прямоугольного треугольника по оси х катет 2 по оси у катет 4
Ответ 2·4/2=4