Найти наибольшее и наименьшее значение функции f(x) ** заданном интервале: f(x)=2x^3 -...

Question

Найти наибольшее и наименьшее значение функции f(x) на заданном интервале: f(x)=2x^3 - 12x^2 + 18x + 3; [-1;2]

Answer 1

f'(x)=6x^2 - 24x + 18

f'(x)=0

6x^2 - 24x + 18=0

можно обе части поделить на 6

x^2 - 4x + 3=0

D^2=16-13=4

D=2

x1=(4-2)/2=1

x2=(4+2)/2=3

от минус бесконечности до 1 f'(x)>0, функция возрастает,

от 1 до 3 1 f'(x)<0 функция убывает</p>

от 3 до плюс бесконечности f'(x)>0, функция возрастает,

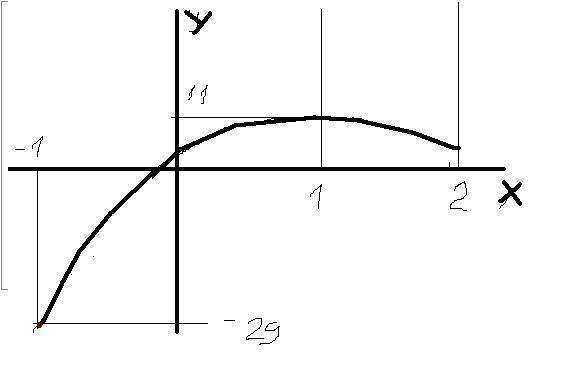
На промежутке от [-1;2]

наибольшее значение функции в точке 1

2*1^3 - 12*1^2 + 18*1 + 3=11

наименьшее в точке -1

2*(-1)^3 - 12*(-1)^2 + 18*(-1) + 3=-29

приблизительно, как на рисунке, только поаккуратнее :-)

---

Answer 2

2x^3-12x^2+18x+3 возьмём производную этого уравнения

 

6x^2-24x+18=0

D=144

x1,2=24-+12/12=  x1=1;x2=3(не удвл)

 

f(1)=2*1-12*1+18*1+3=11

 

f(2)=2*8-12*4+18*2+3=7

 

f(-1)=2*(-1)-12*1+18*(-1)+3=-29

из этого следует что (-29) наим, а (11) наиб )

поспешил людей насмешил ))